In this part we will dive into the basics mathematical side of Cryptography and we will learn about some old Cryptosystems that were used. Underlying the birth of modern cryptography is a great deal of fascinating mathematics,
some of which has been developed for cryptographic applications.
First we will start by discussing Simple Substitution Ciphers, We will now learn one of the simplest methods for encrypting text, the substitution cipher.
Substitution Ciphers
The goal of the Substitution Cipher is the encryption of text, The idea behind a Substation Cryptosystem is very simple: We we simply substitute each letter of the alphabet with another one.
Caesar cipher is one of the simplest and most widely known encryption techniques. It is a type of substitution cipher in which each letter in the plaintext is replaced by a letter some fixed number of positions down the alphabet
Wikipedia
Consider this example of Caesar Cipher.
Example 3.1: Consider we Have this plaintext Hello World and the following encryption Table which is a randomly chosen permutation of the 26 letters in the alphabet In order to encrypt our message.
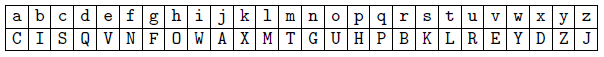
So the process is very simple we just map the letters according to the table so we get the following message OVMM YUBMQ.
Decryption is the same process in order to decrypt the above ciphertext it’s obvious we have to inverse the process.

if we do the same process now we will easily recover the plaintext.
Now let’s see some mathematical properties of substitution cipher, Let’s first start by asking a question How many different simple substitution ciphers exist? We can count them by enumerating the possible ciphertext values for each plaintext letter. we have 26 letters for the ciphertext, So there are 26 possibilities for a, we may assign b to any one of the remaining 25 ciphertext letters. so we get 26 . 25 = 650 possible ways to assign a and b, and the remaining 24 ciphertext letters. And so on so we have 26! = 403291461126605635584000000
Despite the large number of the possible substitution ciphers, they are quite easy to break. The Cryptography analysis Algorithm is used for this purpose. First we get the frequency of the letters in English it’s available online or from this table.

Second we get the frequency of the letters in our ciphertext, and then assign the most frequent letter in English to our most frequent letter and sometimes we can guess the letter we keep this process until we get the plaintext.
Divisibility and Greatest Common Divisors
Modern cryptography is built on foundations of algebra and
number theory. So before we explore modern public key cryptography algorithms, we need the basics to build upon it.
Let’s start by explaining what divisibility is, we say that a is divisible by b if a = cb where c is constant we write that b|a to indicate the b divides a, this symbol | mean divides.
Example 3.2. We have 25 | 125, since 125 = 25 . 5. Note that every integer is divisible by 1, and any integer is not divisible by 2 is odd integer.
proof if a|b and b|c then a|c, this very good proof to give us more understanding on what’s divisibility.
if 1- b = a . r , r is a constant
2- c = b . k , k is constant
then by substitution 1 on 2 we get the following c = a . r . k where k , r are two constants and this completes our proof.
Now to interesting part Greatest common divisor (gcd), we say that two integers a, b have greatest common divisor if there’s positive integer c that divides them both, the greatest common divisor of a, b is denoted by gcd(a, b).
Example 3.3. The gcd of 12, 18 is 6 we got 6 by factoring the numbers 12, 18,
12 = {1, 2, 3, 4, 6, 12}
18 = {1, 2, 3, 6, 9, 18}
so the greatest common integer is 6. this is not scalable method as we will see in a little there’s a better algorithm called Euclidean algorithm. to understand Euclidean algorithm we need to understand Division with remainder.
Let a and b be positive integers. Then we say that a divided by b has quotient q and remainder r if
a = b . q + r , 0 <= r < b
we can write any Integer in the remainder format.
Example 3.4 . Consider the number 125 divided by 4 we can write it in the above format.
125 = 31 . 4 + 1
Now let’s go back to Euclidean algorithm and explain the algorithm behind it, first you should know that Euclidean algorithm is nothing more than repeated division with remainder. without further talking let’s take an example.
Example 3.5. compute gcd(2024, 748) ,a = 2024 , b = 748 using the Euclidean algorithm.
2024 = 748 . 2 + 528
748 = 528 . 1 + 220
528 = 220 . 2 + 88
220 = 88 . 2 + 44 <- gcd = 44
88 = 44 . 2 + 0
The Algorithm works as follows :
- let r_0 = a, r_1 = b
- set i = 1
- divide r_i-1 by r_i to get remainder r_i+1 and quotient q_i
- if r_i+1 = 0 end and the gcd(a,b) = ri
- otherwise r_i+1 > 0 set i = i + 1 and go to step 3
here’s a python code for Euclidean algorithm
def computeGCD(x, y):
while(y):
x, y = y, x % y
return x
a = 60
b= 48
# prints 12
print ("The gcd of 60 and 48 is : ",end="")
print (computeGCD(60,48))
Modular Arithmetic
Definition of Modulo Operation, Let a, r, m be Integers and m > 0. We write a ≡ r mod m, if m divides a – r. m is called modulus and r is called the remainder
Example 3.6. 12 ≡3 mod 9, 3 is valid remainder since 9|(12-3)
for a given module m it does not matter which element from a class we choose for a given computation because all elements of a given equivalence class behave equivalently.
Example 3.7. The Equivalence class for 6:
{…, -18, -12 , -6 , 0 , 6, 12, 18, …}
{…, -17, -11 , -5 , 1 , 7, 13, 19, …}
{…, -16, -10 , -4 , 2 , 8, 14, 20, …}
{…, -15, -9 , -3 , 3 , 9, 15, 21, …}
{…, -14, -8 , -2 , 4 , 10, 16, 22, …}
{…, -13, -7 , -1 , 5 , 11, 17, 23, …}
Well that’s it for this part, please if you have any question or idea to improve my articles feel free to e-mail me on omarobaniessa@gmail.com